在观察经济社会活动时往往需要用到多项统计指标，如考察国家宏观经济运行状况，通常会用到国内生产总值、失业率、居民消费价格、进出口等指标，这些指标间一般存在内在的联系，研究多项指标间的相互依赖关系和内在统计规律性是多元统计分析的基本内容。
一、基本概念
多元统计分析是从经典统计学中发展起来的一个分支，是一种综合分析方法，它能够在多个对象和多个指标互相关联的情况下分析它们的统计规律，在研究经济社会现象中具有广泛应用。
在研究经济社会现象时，会收集大量个体的多方面信息，特别是随着信息化发展，采集到的个体数量和指标数量大大增加。对这些规模宏大、复杂难辨的信息进行提炼简化，提取重要信息辅助决策，是多元统计分析的重要应用领域。同时，经济社会现象间往往存在紧密的联系，表现为统计指标之间存在相关性、因果关系等，使用多元统计分析有助于研究统计指标间的内在联系，发现经济社会现象的内在规律性。
在实际观测和调查中，统计指标的取值一般是随机的，因此统计指标可以用随机变量来表示，那么多个统计指标对应多个随机变量。而多个随机变量组成的数据集合称为随机向量，随机向量服从一定的统计分布，这是多元统计分析方法建立的重要基础。
二、常用方法
多元统计分析方法按照分析特点大致可以分为两类：一是描述性方法，主要从原始数据中提取重要信息，对系统主要特征进行研究，包括主成分分析、因子分析、聚类分析、对应分析等。二是解析性方法，主要是研究变量间相关关系、因果关系等，通过建立模型对变量间的关系认识定量化，包括多元回归分析、判别分析、典型相关分析等。
（一）描述性方法
1．主成分分析
研究某一问题时，往往需要收集多个变量，而这些变量之间通常存在较强的相关关系，直接用它们进行分析，会由于变量之间存在的多重共线性而引起较大的误差。通过主成分分析法可以找到几个主成分来代表原来的多个变量，同时使它们尽可能保留原始变量的信息。这些主成分彼此不相关，数量远少于原始变量的个数，从而达到数据降维的目的。比如，可以通过主成分分析方法在众多变量中进一步确定对地区经济增长最有影响力的变量，即主成分。
2．因子分析
因子分析与主成分分析类似，都是要找出少数几个新的变量来代表原始变量，不同之处主要在于主成分分析中的主成分个数与原始变量个数一致，只不过最后人为将代表大多数变量信息的几个变量确定为少数几个主成分而已；而因子分析则需要事先确定要找几个因子，然后将原始变量综合为少数的几个因子。因子分析可以看作是主成分分析的推广，主成分分析可以看作因子分析的一个特例，因子分析研究更深入、细致，计算上更复杂，实际中应用更广泛。比如，消费者选择购买某一商品的决定因素有很多，某品牌可以通过因子分析法将这些因素综合确定为品牌声誉、产品性能、产品价格3个指标，再针对这3个方面着力提升自身。
3．聚类分析
聚类分析是将具有相似特征的个体归为一类，从而使同类的个体相似性较高，而不同类的个体之间差异较大。衡量个体之间相似性采用“距离”测度和相似系数，常用的“距离”测度有明式距离、马氏距离、兰氏距离，常用的相似系数有夹角余弦、相关系数。聚类分析中常用的方法有系统聚类、动态聚类等。比如，对全国省区市经济类型进行分类时，一般会选取一些经济指标，然后利用这些经济指标计算地区与地区之间的“距离”，将“距离”近的地区归为一类，将“距离”远的地区归为不同类别，从而形成不同地区经济发展水平类别，深化对地区经济的认识。
（二）解析性方法
1．多元回归分析
多元回归分析主要是研究一个因变量与多个自变量之间相互依存关系和数量关系，从而解释、估计和预测因变量的变化。当因变量与各自变量之间为线性关系时，称为多元线性回归。多元回归分析被广泛应用于解释和预测各种经济现象，如在预测长期经济增长趋势时，通常将国内生产总值作为因变量，资本存量、就业人数、人力资本存量、制度变量等作为自变量，利用多元回归分析方法建立经济增长与相关因素的定量模型，根据模型关系对未来经济增长趋势进行预测。
2．判别分析
判别分析是判别观察个体所属类别的一种统计分析方法，它是在已知观察个体分为若干个类别的条件下，通过建立判别规则，对观察个体进行判别分类。它与聚类分析最大不同是，聚类分析事先不知道观察个体有多少个类别，而判别分析事先已知观察个体的类别个数。常用的判别分析法有距离判别法、费舍尔判别法、贝叶斯判别法等。比如，世界银行将全球国家划分为高收入国家、中高收入国家、中低收入国家、低收入国家四种类型，当判断一个国家属于哪种类型时，可以使用判别分析方法建立规则进行判别。
三、示例
为了反映和解释人均可支配收入是怎样被决定的，可以以居民人均可支配收入作为因变量DI，以人均GDP和时间变量T（表征其他影响因素）作为自变量，利用近年居民人均可支配收入和人均GDP数据，建立回归模型：
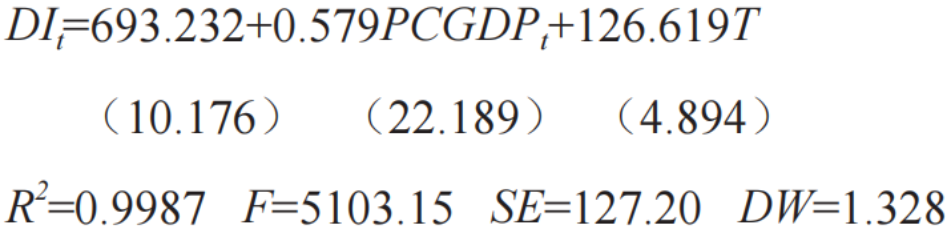导干部基本统计知识问答
模型各项检验均具有显著性，说明该模型具有较强解释能力。模型表明人均GDP每增加1元，居民人均可支配收入可增加0.579元，同时受其他因素影响，人均可支配收入每年可增加126.619元。
