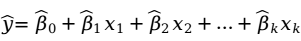设因变量为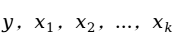 为影响因变量
为影响因变量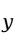 的
的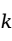 个自变量。描述
个自变量。描述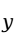 与
与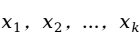 之间线性关系的数学结构式,即多元线性回归模型(multiple linear regression model)为:
之间线性关系的数学结构式,即多元线性回归模型(multiple linear regression model)为:
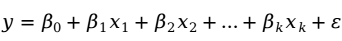
其中,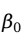 为回归常数;
为回归常数;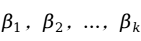 为回归系数;
为回归系数;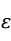 为随机误差项。显然当
为随机误差项。显然当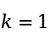 时,即为一元线性回归模型。
时,即为一元线性回归模型。
模型表示 与
与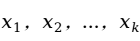 之间的关系可以用两个部分描述:一部分是由于
之间的关系可以用两个部分描述:一部分是由于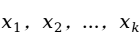 的变化引起
的变化引起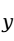 的变化的部分
的变化的部分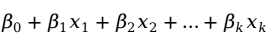 ;另一部分是由除去
;另一部分是由除去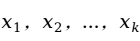 外的其他一切被忽略的、没有考虑到的因素引起的变化及数据的测量误差等,即
外的其他一切被忽略的、没有考虑到的因素引起的变化及数据的测量误差等,即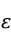 随机误差项。对随机误差项
随机误差项。对随机误差项 的三个基本假定与一元线性回归模型是相同的。
的三个基本假定与一元线性回归模型是相同的。
对上式两边求数学期望得:
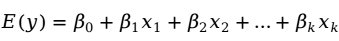
理论回归模型中的参数是未知的,回归分析的主要任务就是通过样本观测值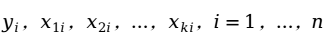 对
对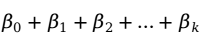 进行估计,在此用
进行估计,在此用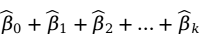 分别表示
分别表示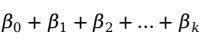 的估计值。这样就得到了估计的多元线性回归方程(multiple linear regression equation)。
的估计值。这样就得到了估计的多元线性回归方程(multiple linear regression equation)。