回归方程的显著性检验主要是检验因变量和自变量之间的线性关系是否显著。对于一元线性回归模型而言，如果回归函数
中
，则无论
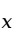怎么变化，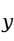
都不随着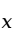
的变化而变化，此时认为回归方程不显著，说明回归方程的线性关系是不存在的。否则，如果
，说明回归方程的线性关系是存在的。
所以，对于一元线性回归模型而言，回归方程的总体显著性检验等价于回归系数
的显著性检验。即检验如下的假设：
(两个变量之间线性关系不显著)
(两个变量之间的线性关系显著)
通常有两种方法进行检验：
检验法和
检验法。
1.
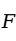检验法
当原假设成立时，统计量：
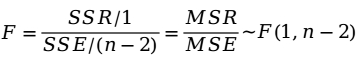
其中，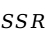
为回归平方和；
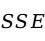为残差平方和；
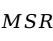为回归均方（是回归平方和除以相应的自由度，在一元回归中自由度是1）；
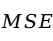为残差均方（是残差平方和除以相应的自由度，在一元回归中自由度是
）。
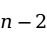最后，根据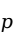
值进行判断：如果
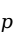值小于我们事前确定的显著性水平
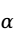时，拒绝原假设，认为
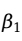是不为零的，回归方程的线性关系是存在的。否则，不能拒绝原假设，即回归方程不存在线性关系。
2.
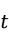检验法
当原假设成立时，统计量：
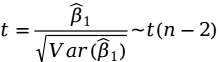
其中，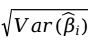
为回归系数的标准差。
判定的标准与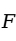
检验相同，也是看
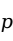值是否小于我们事前确定的显著性水平
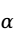来判断线性关系的存在与否。
