由于样本的随机性、样本数量少等原因,利用样本数据计算出来的相关系数不能直接说明总体变量之间是否存在显著相关,需要进行统计检验。相关系数的检验通常用 Fisher 提出的 ![]() 分布检验,该检验可以用于小样本,也可以用于大样本。该检验的具体步骤如下:
分布检验,该检验可以用于小样本,也可以用于大样本。该检验的具体步骤如下:
第1步:提出原假设。
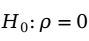 (两变量之间不存在线性相关)
(两变量之间不存在线性相关)
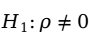 (两变量之间存在线性相关)
(两变量之间存在线性相关)
第2步:计算检验的统计量。
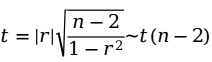
第3步:进行决策。
根据给定的显著性水平(一般取![]() )和自由度(这里是取
)和自由度(这里是取![]() )计算临界值,如果
)计算临界值,如果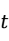 检验统计量的值落在拒绝域内,则拒绝原假设,可以认为两个变量之间存在显著的相关关系。或者利用统计软件直接得到
检验统计量的值落在拒绝域内,则拒绝原假设,可以认为两个变量之间存在显著的相关关系。或者利用统计软件直接得到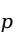 值,如果
值,如果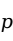 值小于等于指定的显著性水平,则我们可以拒绝原假设,接受备择假设,即这两个变量之间存在线性相关关系。否则不能拒绝原假设,可以认为两变量之间不存在显著的线性相关关系。
值小于等于指定的显著性水平,则我们可以拒绝原假设,接受备择假设,即这两个变量之间存在线性相关关系。否则不能拒绝原假设,可以认为两变量之间不存在显著的线性相关关系。




