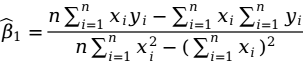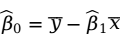回归直线能代表两个变量之间的关系,那如何来找到最佳的一条直线呢?回归直线由它的截距项和斜率所确定,那么寻找这条回归直线的过程就是估计回归模型中回归系数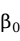 和
和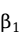 的过程。如果我们每个人都拿一把尺子去比对散点图作一条通过这些点的中心的直线,每个人会做一条稍微不同的直线,显然离所有的点距离最近的直线是最好的直线。最常用的统计准则是普通最小二乘法(ordinary least square,简称OLS),其思想就是寻找一条直线,使得所有观测点(
的过程。如果我们每个人都拿一把尺子去比对散点图作一条通过这些点的中心的直线,每个人会做一条稍微不同的直线,显然离所有的点距离最近的直线是最好的直线。最常用的统计准则是普通最小二乘法(ordinary least square,简称OLS),其思想就是寻找一条直线,使得所有观测点(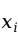 ,
,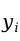 )与它在回归直线上的对应点
)与它在回归直线上的对应点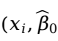 +
+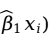 ,在垂直方向上的偏差距离平方和最小(如图6-2所示)。这里的垂直方向的偏差就是残差,即观测值
,在垂直方向上的偏差距离平方和最小(如图6-2所示)。这里的垂直方向的偏差就是残差,即观测值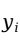 与回归拟合值
与回归拟合值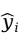 之间的差
之间的差

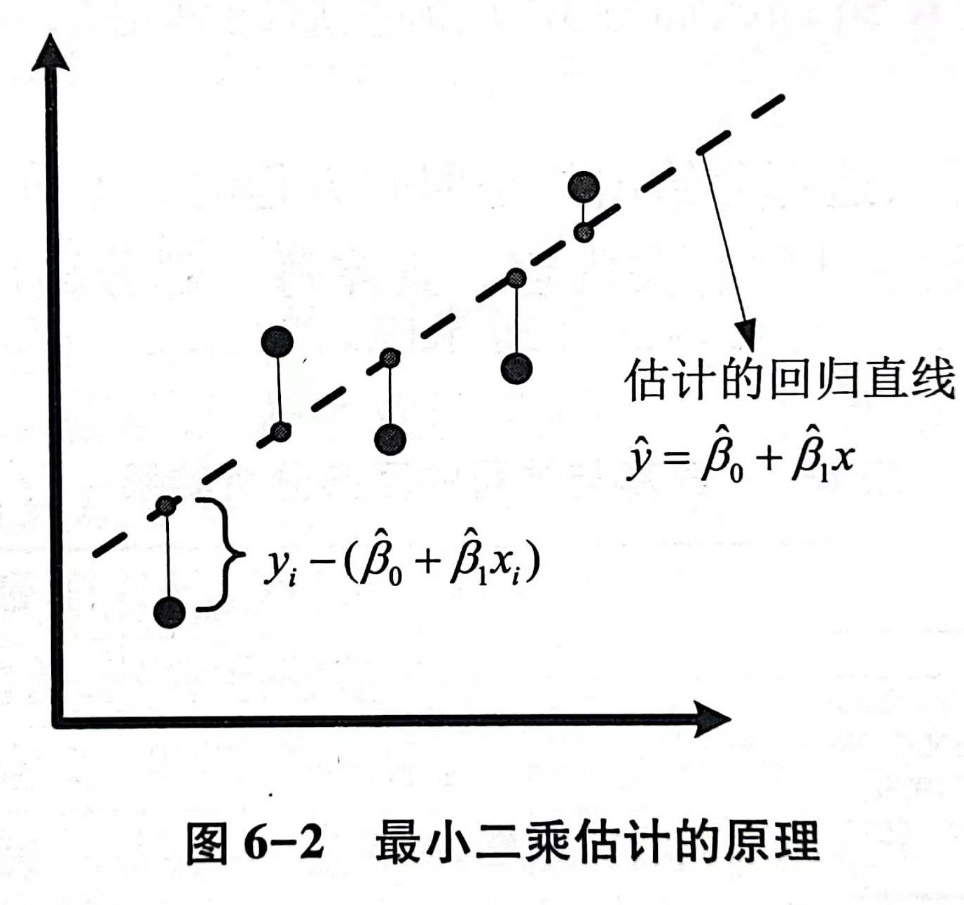
对每个样本观测值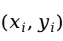 ,考虑观测值
,考虑观测值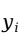 与其回归直线拟合值
与其回归直线拟合值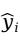 的离差
的离差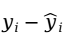 (即残差)越小越好,综合地考虑n个离差值,定义离差平方和(残差平方和)为:
(即残差)越小越好,综合地考虑n个离差值,定义离差平方和(残差平方和)为:
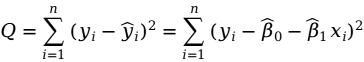
所谓最小二乘法,就是要寻找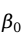 和
和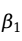 的估计值
的估计值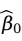 和
和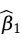 ,使Q达到最小。求解
,使Q达到最小。求解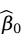 和
和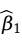 是一个求极值问题,由于Q是关于
是一个求极值问题,由于Q是关于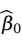 和
和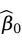 的非负二次函数,因而它的最小值总是存在的。根据微积分求极值的原理,
的非负二次函数,因而它的最小值总是存在的。根据微积分求极值的原理,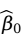 ,
,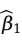 满足下列方程:
满足下列方程:
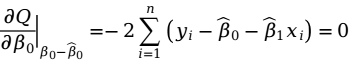
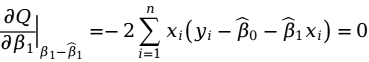
求解该方程组,即可得到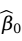 和
和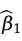 。
。
对于一元线性回归方程,其参数估计值的具体计算公式为: