四分位距(interquartile)是上下四分位数之差,也称为样本的内距或四分位差,用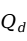 表示。其计算公式为:
表示。其计算公式为: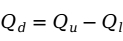
四分位距反映了中间50%数据的离散程度,其数值越小,说明中间的数据越集中;其数值越大,说明中间的数据越分散。四分位距不受极值的影响。此外,由于中位数处于数据的中间位置,因此四分位距的大小在一定程度上也说明了中位数对一组数据的代表程度。四分位距主要用于测度顺序数据的离散程度。对于数值型数据也可以计算四分位距,但它不适合分类数据。


四分位距(interquartile)是上下四分位数之差,也称为样本的内距或四分位差,用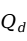 表示。其计算公式为:
表示。其计算公式为: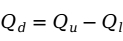
四分位距反映了中间50%数据的离散程度,其数值越小,说明中间的数据越集中;其数值越大,说明中间的数据越分散。四分位距不受极值的影响。此外,由于中位数处于数据的中间位置,因此四分位距的大小在一定程度上也说明了中位数对一组数据的代表程度。四分位距主要用于测度顺序数据的离散程度。对于数值型数据也可以计算四分位距,但它不适合分类数据。
四分位距(interquartile)是上下四分位数之差,也称为样本的内距或四分位差,用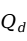 表示。其计算公式为:
表示。其计算公式为: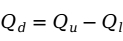
四分位距反映了中间50%数据的离散程度,其数值越小,说明中间的数据越集中;其数值越大,说明中间的数据越分散。四分位距不受极值的影响。此外,由于中位数处于数据的中间位置,因此四分位距的大小在一定程度上也说明了中位数对一组数据的代表程度。四分位距主要用于测度顺序数据的离散程度。对于数值型数据也可以计算四分位距,但它不适合分类数据。
[责任编辑:]

