两个总体比例之差的假设检验分为检验两个总体比例是否相等的假设,即检验两个总体比例之差为零的假设,以及检验两个总体比例之差不为零的假设。由样本比例的抽样分布可知,从两个二项分布的总体中抽出两个独立的样本,则两个样本的比例之差的抽样分布服从正态分布。设两个总体中具有某种特征的单位数所占的比例分别为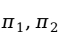 ,来自这两个总体的样本(样本容量分别为
,来自这两个总体的样本(样本容量分别为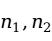 )中具有该种特征的单位数分别为
)中具有该种特征的单位数分别为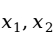 ,所占的比例分别为
,所占的比例分别为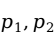 。即,
。即,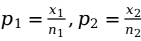 。
。
(一)检验两个总体比例是否相等的假设
在这种情况下,检验的假设为:

在原假设成立的条件下,最佳的方差是将两个样本合并后得到的合并比例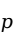 ,其计算公式为:
,其计算公式为:
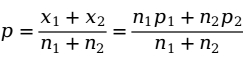
在大样本条件下,两样本的比例之差服从正态分布,可得检验统计量的表达式为:
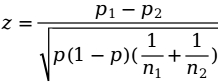
(二)检验两个总体比例之差是否等于某个常数
在这种情况下,检验的假设为:
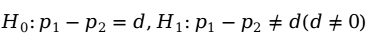
可直接用两个样本比例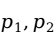 作为两个总体比例
作为两个总体比例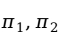 的估计量。在大样本情况下,可以得到两个样本比例之差的抽样分布为:
的估计量。在大样本情况下,可以得到两个样本比例之差的抽样分布为:
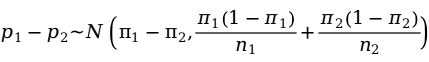
这样两个总体比例之差的假设检验统计量为:
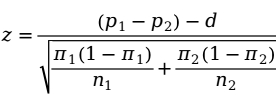
当总体比例未知时,通常用样本比例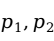 代替上式中的
代替上式中的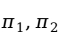 ,此时的检验统计量为:
,此时的检验统计量为:





