1.大样本估计
如果两个样本是从两个总体中独立抽取的,即一个样本中的元素与另一个样本中的元素相互独立,则称为独立样本(independent sample)。如果两个总体均为正态分布,或两个总体不服从正态分布但两样本均为大样本,则两个总体均值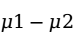 之差在
之差在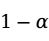 置信水平下的置信区间为:
置信水平下的置信区间为:
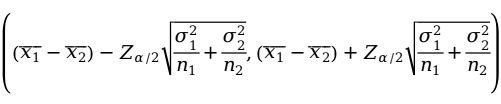
当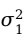 和
和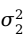 未知时,可用样本方差
未知时,可用样本方差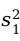 和
和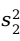 来代替,此时两个总体均值
来代替,此时两个总体均值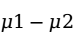 之差在
之差在 置信水平下的置信区间为:
置信水平下的置信区间为:
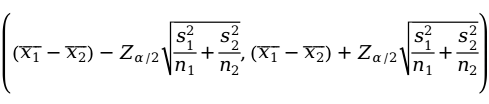
2.小样本的估计
当两样本均为小样本时,为估计两个总体的均值之差,需假定两个总体均为正态总体,且两个随机样本独立地分别抽自两个总体。在上述假定下,无论样本容量的大小,两个样本均值之差均服从正态分布。
(1)当两个总体方差 和
和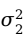 已知时,可建立两个总体均值之差的置信区间。
已知时,可建立两个总体均值之差的置信区间。
(2)当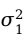 和
和 未知时,有以下几种情况:
未知时,有以下几种情况:
①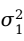 =
=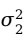 ,两个样本均值之差经过标准化之后服从自由度为
,两个样本均值之差经过标准化之后服从自由度为 的
的 分布,两个总体的均值之差
分布,两个总体的均值之差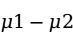 在
在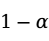 置信水平下的置信区间为:
置信水平下的置信区间为:
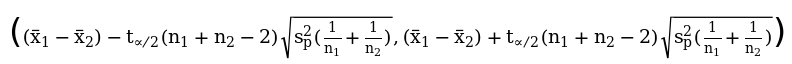
其中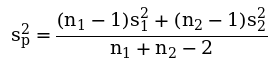 。
。
② ≠
≠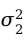 ,两个样本均值之差经过标准化之后近似服从自由度为
,两个样本均值之差经过标准化之后近似服从自由度为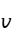 的
的 分布,两个总体的均值之差
分布,两个总体的均值之差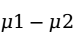 在
在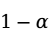 置信水平下的置信区间为:
置信水平下的置信区间为:
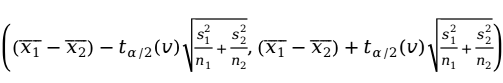
其中,自由度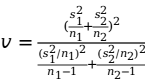 。
。


