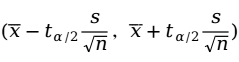均值的区间估计

在对总体均值进行区间估计时，需要考虑总体是否为正态分布、总体方差是否已知、用于估计的样本是大样本还是小样本等几种情况。但不管哪种情况，总体均值的置信区间都是由样本均值加减估计误差得到的。一般将置信水平表示为，统计量分布两侧面积各为的分位数值，它取决于事先所要求的置信度（或可靠程度）。因此总体均值在置信水平下的置信区间可一般性地表达为：

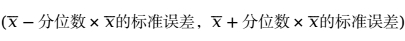
1.大样本的估计

在大样本情况下，由前述可知样本均值服从期望值为、方差为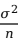的正态分布。因此，当总体方差已知时，总体均值在置信水平下的置信区间为：

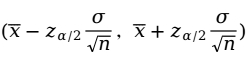
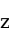式中，为事先确定的一个概率值，它是总体均值不包括在置信区间的概率；为置信水平；为标准正态分布上两侧面积各为时的值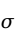；为总体的标准差；为估计误差。

当总体方差未知时，上式中的可以用样本方差代替，这时总体均值在置信水平下的置信区间为：

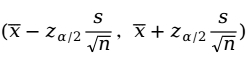
2.小样本的估计

在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定前提下。如果正态总体的已知，样本均值经过标准化后仍服从标准正态分布，此时仍可用上式建立总体均值的置信区间；如果正态总体的未知，样本均值经过标准化后服从自由度为的分布。即：

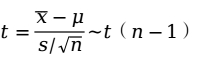
分布也是对称分布，只不过计算出来的值对应的概率要查分布概率表或根据统计软件计算得到。在置信水平下，总体均值的置信区间为：