点估计就是直接用样本数据计算出来的统计量当做总体参数的估计值。可用于总体参数点估计的估计量可以有很多。比如,可以用样本均值作为总体均值的估计量,也可以用样本中位数作为总体均值的估计量,等等。那么,用哪种估计量作为总体参数的估计呢?自然要用估计效果最好的那种估计量。什么样的估计量才算是一个好估计量呢?这就需要有一定的评价标准。统计学家给出了评价估计量的一些标准,主要包括下列三个:
(一)无偏性
无偏性(unbiasedness)是指估计量抽样分布的期望值等于被估计的总体参数。设总体参数为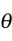 ,所选择的估计量为
,所选择的估计量为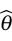 ,如果
,如果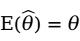 ,则称
,则称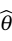 为
为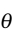 的无偏估计量。由样本均值的抽样分布可知,
的无偏估计量。由样本均值的抽样分布可知,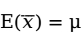 ,
,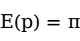 ,同样可以证明,
,同样可以证明,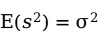 。因此,
。因此,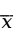 ,
, ,
,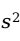 分别是总体均值
分别是总体均值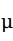 、总体比例
、总体比例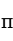 、总体方差
、总体方差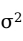 的无偏估计量。
的无偏估计量。
(二)有效性
有效性(efficiency)是指估计量的方差尽可能小。一个无偏的估计量并不意味着它就非常接近被估计的总体参数,估计量与参数的接近程度是用估计量的方差(或标准误差)来度量的。对同一个总体参数的两个无偏估计量,有更小方差的估计量更有效。假定有两个用于估计总体参数的无偏估计,分别用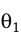 、
、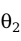 表示,它们的抽样分布的方差分别用
表示,它们的抽样分布的方差分别用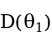 和
和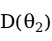 表示,如果
表示,如果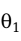 的方差小于
的方差小于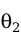 的方差,即
的方差,即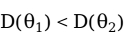 ,就称
,就称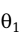 是比
是比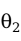 更有效的一个估计量。
更有效的一个估计量。
(三)一致性
一致性(consistency)是指随着样本量的增大,估计量的值越来越接近被估计总体的参数。换言之,一个大样本给出的估计量要比一个小样本给出的估计量更接近总体的参数。由于样本均值的标准误差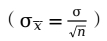 与样本量大小有关,样本量越大,
与样本量大小有关,样本量越大,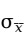 的值就越小。因此可以说,大样本量给出的估计量更接近于总体参数。从这个意义上说,样本均值是总体均值的一个一致估计量。
的值就越小。因此可以说,大样本量给出的估计量更接近于总体参数。从这个意义上说,样本均值是总体均值的一个一致估计量。




